Actividades

1º.- Utiliza los desarrollos de los 5 polígonos regulares y constrúyelos.

2º.- Utilizando los poliedros que has construido en el apartado anterior o los applets de Descartes de la página "Fórmula de Euler", completa la siguiente tabla y comprueba que todos los sólidos platónicos cumplen la fórmula de Euler.

	Vértices	Caras	Aristas
tetraedro
octaedro
icosaedro
hexaedro
dodecaedro

3º.- Los siguientes poliedros se han obtenido suprimiendo una parte de un hexaedro.

       

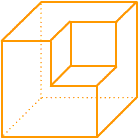
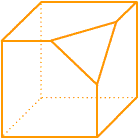
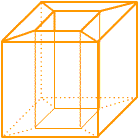
Completa la siguiente tabla y comprueba si verifican la fórmula de Euler

	Vértices	Caras	Aristas
Figura 1
Figura 2
Figura 3

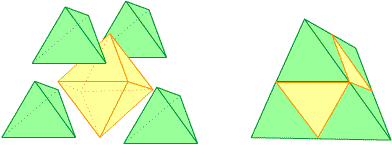
4º.- Construye un octaedro regular y cuatro tetraedros, únelos como indica la figura. ¿Qué nuevo poliedro obtienes?

5º.- Si observas detenidamente un balón de fútbol comprobarás que es un poliedro con caras hexagonales y pentagonales. En cada vértice confluyen dos hexágonos y un pentágono. Si cuentas sus caras verás que tiene 17 hexágonos y 15 pentágonos, con un total de 78 vértices. Como cumple la fórmula de Euler, ¿cuántas aristas tiene?