|
Ejecución |
 |
|
Guión de la actividad |
|
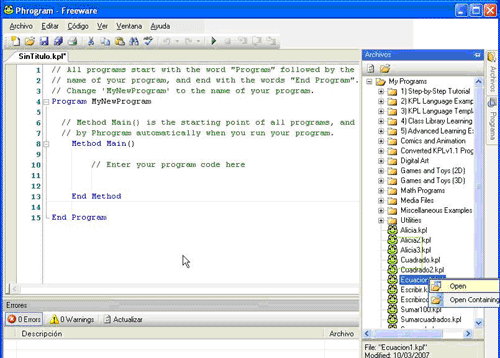
Arrancar el KPL.
Abrimos el archivo
Ecuacion1 creado en la
actividad 8 bien desde la
carpeta My Programs Files
que está en Mis Documentos o
bien desde: |
|
 |
|
Editar el comentario inicial
para que quede así: |
// Programa: Ecuación 2
// Autores: lidia y pablo
// Descripción: este programa nos muestra las soluciones de la
// ecuación de segundo grado, si es que existen
|
|
 |
Poner título al programa:
Ecuacion2.
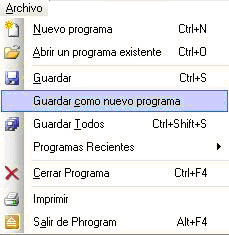
Guardar el archivo picando
en Archivo/Guardar como
nuevo programa:
|
|
y escribiremos el nombre
Ecuacion2, seleccionando
la carpeta donde quiera ir
almacenando todas las
actividades. Por defecto la
carpeta elegida es My
Phrograms Files que está en
Mis Documentos.
En el Método Principal,
Method Main(), añadimos la
variable con tipo de dato
decimal valorc: |
|
|
|
Quitamos valorx y añadimos las líneas: |
Var valorx1
As
Decimal
Var
valorx2
As
Decimal
Var
discriminante
As
Decimal
|
|
para definir las dos variables donde van a estar las
soluciones y la variable
discriminante, que será el
valor del discrimínate de la
ecuación de segundo grado.
Escribimos: |
SetConsoleTextAlignment("center")
|
|
que configura el modo de alineamiento centrado
del texto de la ventana de
consola.
Editamos el código de las
dos líneas siguientes para
que quede: |
ConsoleWriteLine("Vamos
a resolver una ecuación
de segundo grado de la
forma:")
ConsoleWriteLine("
a x^2 + b x + c = 0")
|
|
Dentro del While que tenemos
para asegurarnos que el
usuario introduce un valor
para “a” es distinto de
cero, cambiamos el texto
PRIMER GRADO por SEGUNDO
GRADO.
Después de: |
valorb=ConsoleReadDecimal("Introduzca
el valor de b = ",True)
|
|
tecleamos el código: |
valorc=ConsoleReadDecimal("Introduzca
el valor de c = ",True)
|
|
para asignar a valorc el valor del término
independiente de la ecuación
de segundo grado que
introduzca el usuario a
través de la consola.
Después eliminamos la línea |
valorx=(valorb*-1)/(valora)
|
|
y añadimos: |
discriminante=(valorb*valorb)+(4*(valora)*(valorc*-1))
|
|
con lo que asignamos a la variable
discriminante el
valor
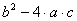 . .
Por último, eliminamos las
dos líneas siguientes y
escribimos el código: |
If discriminante>=0 Then
valorx1=((valorb*-1)+sqrt(discriminante))/(2*(valora))
valorx2=((valorb*-1)+(sqrt(discriminante))*-1)/(2*(valora))
ConsoleWriteLine("")
ConsoleWriteLine("*****DOS
SOLUCIONES REALES*****")
ConsoleWrite("x
= "+valorx1)
ConsoleWriteLine("")
ConsoleWrite("x
= "+valorx2)
If
valorx1=valorx2
Then
ConsoleWriteLine("")
ConsoleWriteLine("***SOLUCIÓN DOBLE***")
End
If
Else
ConsoleWriteLine("")
ConsoleWriteLine("*****NO
EXISTEN SOLUCIONES
REALES*****")
End If
|
|
¿Qué hacemos con esto? La
clave está en el signo del
discriminante. Si el
discriminante es mayor o
igual que cero, sabemos que
la ecuación tiene dos
soluciones reales que son:
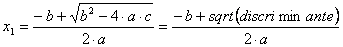
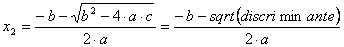
Obsérvese que sqrt es la
función matemática
disponible en KPL que
devuelve la raíz cuadrada.
Si el discriminante es menor
que cero, sabemos que la
ecuación de segundo grado no
tiene solución real.
Así pues, la idea es la
siguiente: |
If discriminante>=0
Then
//existen 2 soluciones
reales
Else
//no existen soluciones
reales
End If
|
|
Además en el caso de que el
discriminante sea mayor o
igual que cero añadimos un
IF para que en el caso de
que las 2 raíces sean
iguales, es decir, el
discriminante cero, el
programa imprima por
pantalla que la solución es
doble.
Guardamos el archivo picando
sobre el icono
 o Archivo/Guardar.
o Archivo/Guardar.
En el caso de existir algún
error en el CÓDIGO FUENTE de
nuestro programa, KPL nos
informa con un aviso de
ERROR y el cursor se sitúa
sobre la línea y secuencia
errónea. Lo rectificaremos.
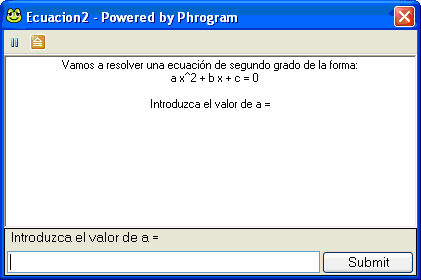
Al ejecutar el programa
(F5), se activa la consola y
nos pide el valor de a: |
|
 |
|
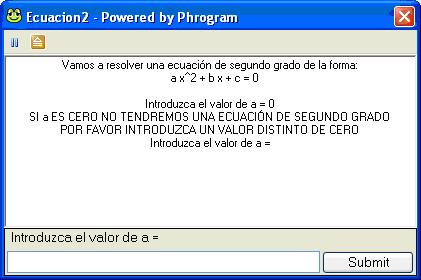
si introducimos 0,
obtenemos: |
|
 |
|
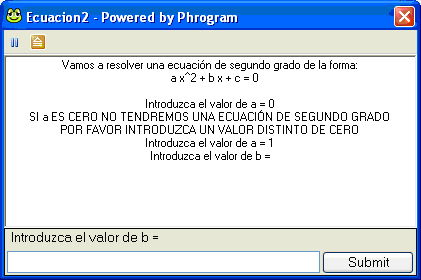
y si ahora introducimos, por
ejemplo, 1 y damos a intro,
nos pedirá el valor de b: |
|
 |
|
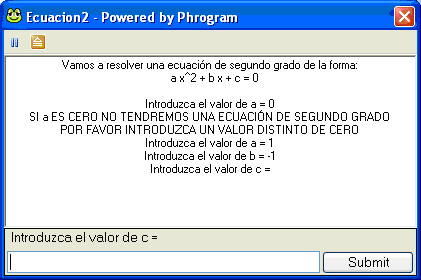
introducir -1, damos a intro,
y después nos pedirá el
valor de c: |
|
 |
|
Introducimos -6 por ejemplo
y la solución es: |
|
 |
|
Puedes probar a ejecutar el programa con distintos valores
para a, b y c, como por
ejemplo:
1)
a = 1, b = 4, c = 4
2)
a = 2, b = -1 c = 5
3)
a = 1, b = 5, c = 6 |

