PROBLEMA 1

Observa los siguientes triángulos construidos sobre un geoplano:

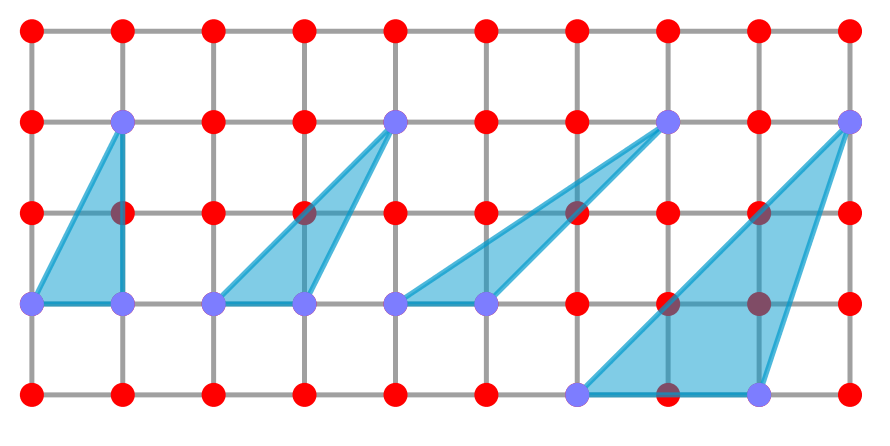
Completa la siguiente tabla para cada triángulo:

	BASE	ALTURA	ÁREA
TRIÁNGULO 1
TRIÁNGULO 2
TRIÁNGULO 3
TRIÁNGULO 4

PROBLEMA 2

Como has podido observar en el ejercicio anterior, base, altura y área están relacionados en un triángulo. Conociendo dos de ellos se puede calcular el tercero. Completa la siguiente tabla:

Base	$2 \,cm$		$1,5 \,cm$
Altura	$2,5 \,cm$	$3 \,cm$		$2 \,cm$
Área		$9 \,cm^2$	$5 \,cm^2$	$2 \,cm^2$

PROBLEMA 3

Ahora te toca a ti construir triángulos. Construye varios triángulos distintos en el siguiente geoplano cuya área sea de $4\, u^2$.

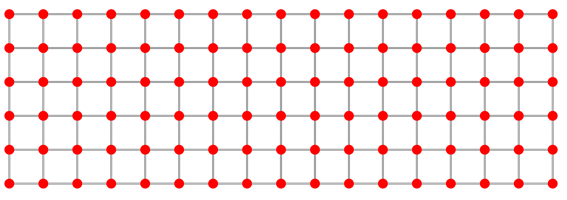
PROBLEMA 4

Dibuja todos los triángulos rectángulos distintos que se puedan hacer en un geoplano de $5 \times 5$. Calcula el perímetro de cada uno de ellos.

PROBLEMA 5

Dado un triángulo cualquiera siempre podemos construir un romboide como se puede ver en la siguiente imagen:

También podemos recortar dos triángulos iguales y superponerlos formando el romboide.

• Describe como hemos construido el romboide.
• ¿Qué relación existe entre el área del romboide y del triángulo?
• Escribe la fórmula que nos daba el área de un romboide.
• Teniendo en cuenta lo anterior, ¿podrías escribir la fórmula del área de un triángulo cualquiera?

PROBLEMA 6

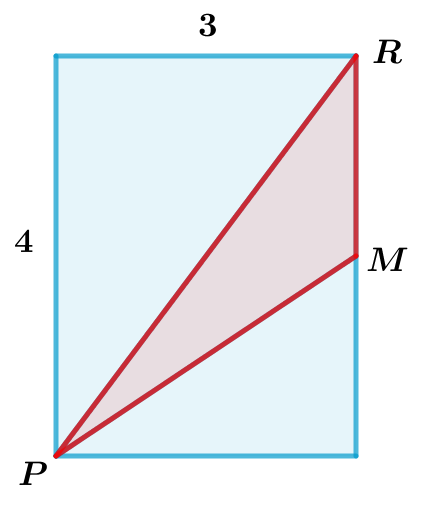
$M$ es el punto medio del lado del rectángulo. ¿Cuál es el área, en unidades al cuadrado, del triángulo $PMR$?