Una función es una relación entre dos conjuntos numéricos, de forma que a cada valor específico del primer conjunto, le corresponde, como mucho, un único valor del segundo conjunto (relación unívoca).
Entonces, podemos entender una función como una máquina que transforma un conjunto de números en otro. La única condición que tiene esta máquina es que los elementos de la entrada solo producen un elemento en la salida, nunca dos o más.
Las funciones se pueden definir de diversas formas, por ejemplo:
A esa \(x\) se le denomina variable independiente porque es aquella cuyos valores elegimos libremente. A la \(y\) se le denomina variable dependiente porque depende y se calcula a partir de la variable \(x\).
Una función también puede verse como una relación o correspondencia entre dos magnitudes, de forma que a cada valor específico de la primera de las magnitudes (independiente) le corresponde, como mucho, un único valor de la segunda magnitud.
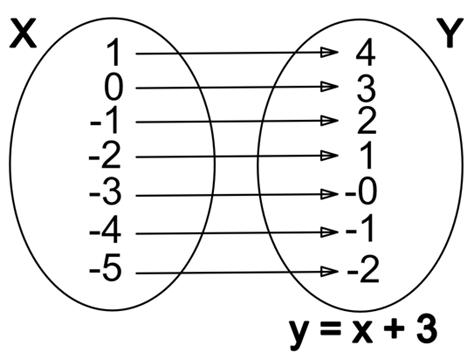
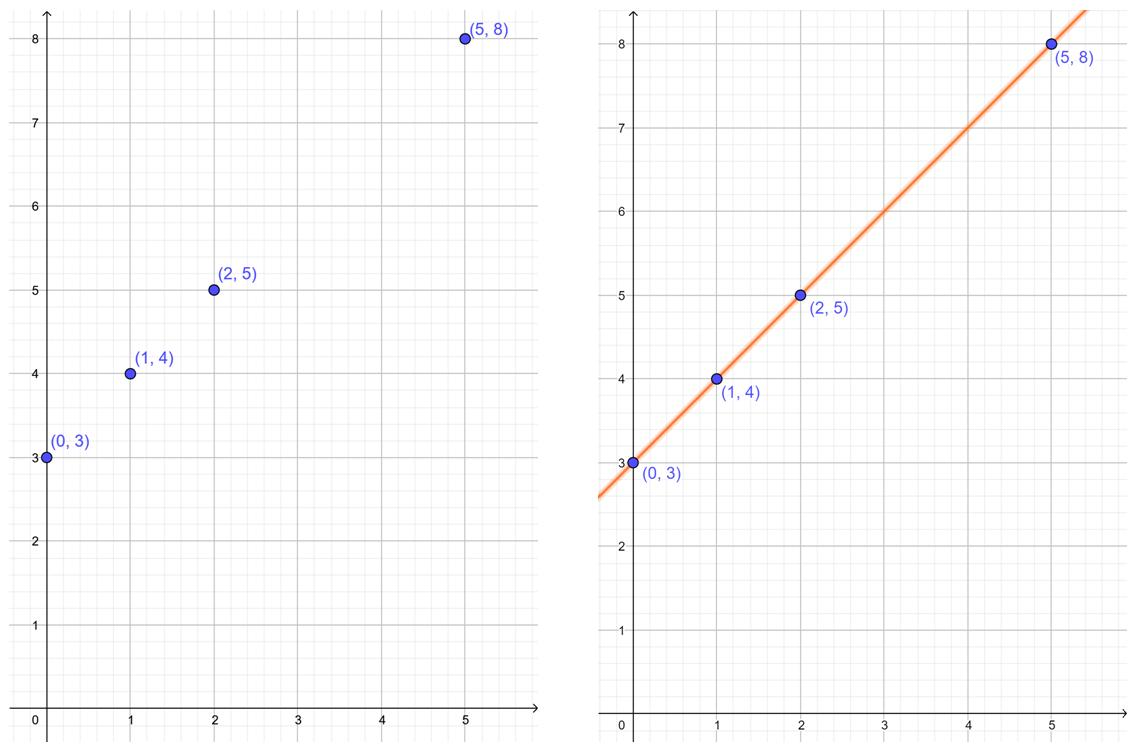
Ejemplo: La longitud de una circunferencia y el radio de la misma.
La longitud de la circunferencia depende del radio de esta; por lo tanto, el radio es la variable independiente y la longitud de su circunferencia la variable dependiente.
Para cada valor del radio, obtenemos una longitud de circunferencia por lo que la relación es funcional.
La expresión algebraica que relaciona ambas magnitudes es \(l=2\cdot \pi \cdot r\). Podemos utilizar esta expresión (o fórmula) para obtener una tabla de valores:
En la gráfica siguiente se observa que todos los puntos están sobre una misma recta. En este caso la razón entre la longitud de la circunferencia y el radio es constante y por tanto son magnitudes proporcionales y su constante de proporcionalidad es \(2\cdot \pi\)
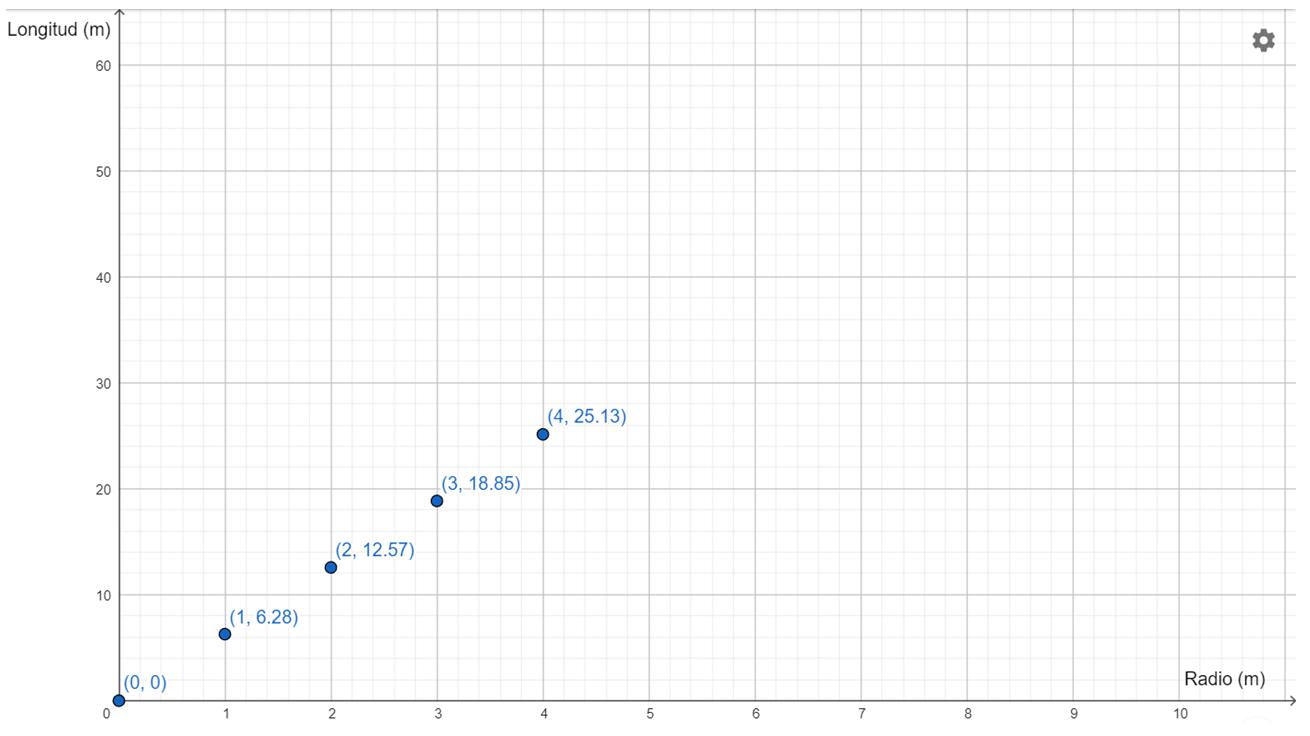
Cualquier otro punto de la función estará alineado con los puntos de la gráfica. Uniendo estos puntos se obtiene la gráfica completa de la función.
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0