Llegados al final del tema reflexiona sobre lo que has aprendido. Marca en la siguiente tabla lo que corresponde a cada frase, haz la autoevaluación y revisa de nuevo la tabla.
Funciones 2º de la ESO
EVALÚA Y AFIANZA
¿CÓMO LO HAGO?
|
Me cuesta hacerlo |
Estoy aprendiendo |
Lo hago bien |
Soy un experto |
|
| Situar puntos en el plano si me dan las coordenadas | ||||
| Escribir las coordenadas de un punto si lo veo en el plano | ||||
| Construir una tabla a partir de un conjunto de pares de datos que aparecen en un problema | ||||
| Establecer ejemplos reales de funciones lineales | ||||
| Representar una función lineal a partir de un enunciado | ||||
| Representar una función lineal a partir de una tabla de valores | ||||
| Representar una función lineal a partir de su expresión algebraica | ||||
| Calcular la pendiente de una recta a partir de la tabla de la función que representa la recta. | ||||
| Escribir la expresión algebraica de una función lineal a partir de su tabla | ||||
| Calcular la pendiente de una recta a partir de su gráfica. | ||||
| Escribir la expresión algebraica de una función lineal a partir de su gráfica | ||||
| Explicar la solución de ejercicios y problemas | ||||
| Comprobar la solución del problema | ||||
| Trabajar en grupo para resolver tareas | ||||
| Aprender de mis errores | ||||
| Enfrentar un reto o tarea con ganas y motivación | ||||
| Esforzarme para hacer bien las tareas |
AUTOEVALUACIÓN
A1. Representa los siguientes puntos en el plano cartesianos: \(\left(3,-5\right)\), \(\left(1,-1\right)\), \(\left(0,1\right)\), \(\left(-2,5\right)\) y \(\left(-3,7\right)\). ¿Siguen un patrón especial esos puntos? Descríbelo.
SOLUCIÓN
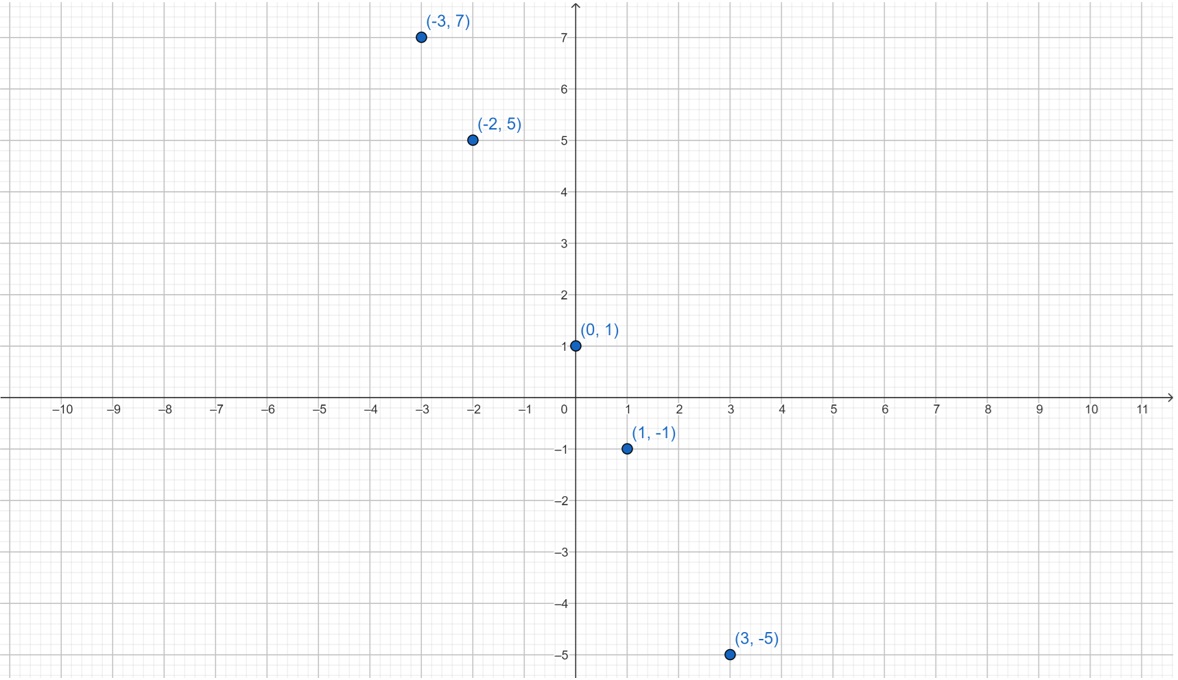
Los puntos están alineados, por lo que se podría trazar una línea recta que pasara por todos ellos.
(Otro tipo de justificación similar también puede ser válida)
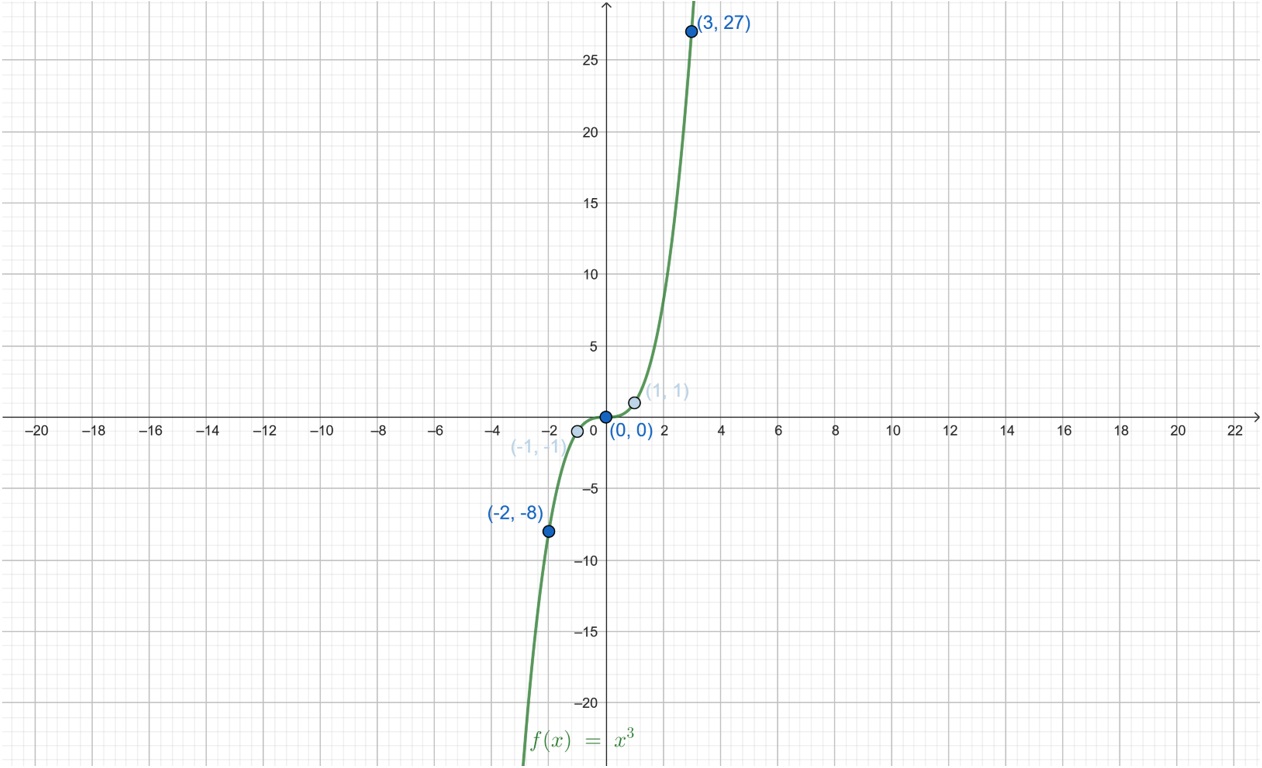
A2. Una función asigna a cada valor su cubo.
PREGUNTAS
-
Escribe su fórmula o expresión algebraica.
-
Halla los valores de la variable dependiente para distintos valores de \(x\). Por ejemplo, para \(x=-2\), \(x=0\) y \(x=3\)
-
Representa la función a partir de los puntos obtenidos en el apartado anterior.
SOLUCIÓN

A3. El siguiente gráfico muestra la distancia que puedo recorrer por cada litro de gasoil que consumo viajando a una velocidad constante de 90 km/h.
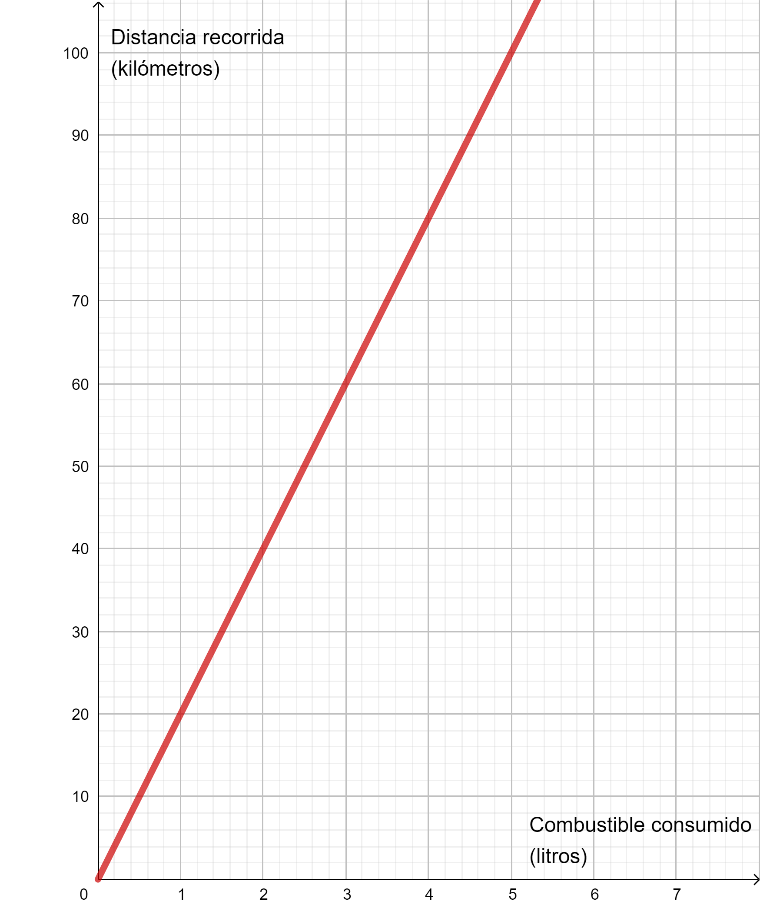
PREGUNTAS
-
Determina cuál es la variable independiente.
-
¿Qué distancia puedo recorrer con 3 litros de gasoil?
-
¿Qué cantidad de combustible necesito para recorrer 80 kilómetros?
-
¿Cuánto me cuesta recorrer 40 kilómetros si el precio del combustible es 1,90 € el litro?
-
Escribe la expresión algebraica para la función de esa gráfica.
SOLUCIÓN
-
El combustible que puedo consumir.
-
60 kilómetros.
-
4 litros.
-
3,80 €
-
\(\boldsymbol{y=20x+0=20x}\)
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0


